در برنامه ریزی درسی ریاضیات دو نوع ارتباط همیشه باید مدنظر برنامه ریز ، مؤلف و حتی معلم باشد :

  1. ارتباط درونی : مفاهیم و مهارتهای ریاضی در درون خود با هم یک ارتباط نزدیک و شبکه ای دارند. برنامه و آموزش باید به شکلی باشد که دانش آموز این ارتباطات و روابط درونی را درک کنند و ریاضیات را به صورت یک پارچه یاد بگیرند.

  2. ارتباط بیرونی : ریاضیات شامل کلیه ارتباطات ریاضی با زندگی روزمره ، سایر علوم و کاربردهایی در زندگی علمی آینده دانش آموز است. به این ترتیب در برنامه درسی و آموزشی ، برقرار کردن پیوند ریاضیات با کاربردهایش در زندگی روزمره و سایر علوم از قبیل هنر ، علوم طبیعی و علوم اجتماعی باید مدنظر قرار گیرد. در صورتی که این موارد در آموزش دیده نشود ، این سوال همیشه در ذهن دانش آموز باقی می ماند که «به چه دلیل ریاضی بخوانیم؟» یا «این ریاضیات به چه درد ما می خورد؟»

شبکه مفهـــومی-  شبکه مهــــارتی

همانطور که اشاره شد ارتباط درونی ریاضیات در برنامه ریزی اهمیت خاصی دارد. هرچه عمق درک و یادگیری مفاهیم ریاضی بیشتر شود ، ارتباط ها و حقایق بیشتری در ذهن ثبت می گردد. به طوری که فرد به یک شهود و کل گرایی نزدیک می شود.

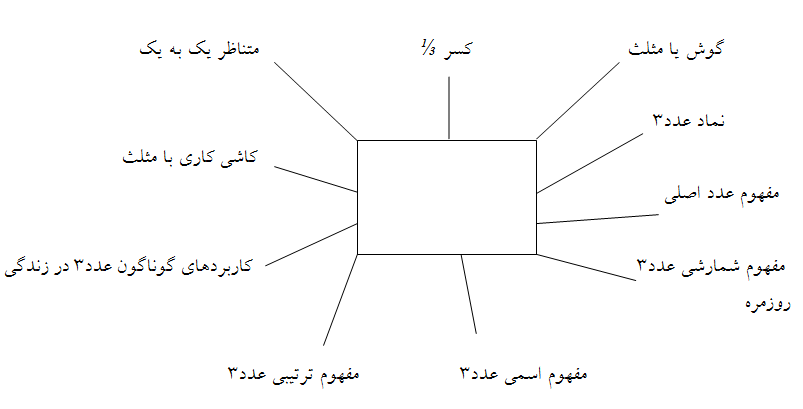
برای رساندن دانش آموزان به بلوغ فکری در حل مسائل ریاضی در برنامه ریزی باید شبکه های مفهومی و شبکه های مهارتی را طراحی کرد. در صورتی که برنامه ریزی به طور شبکه ای یا با تلفیق درونی جنبه های گوناگون ریاضی باشد ، این امر در آموزش به دانش آموز منتقل می شود و دید او را نیز به هم مرتبط خواهد کرد. برای مثال در این رویکرد وقتی قصد داریم مفهوم و نماد 3 به دانش آموز کلاس اول دبستان آموزش دهیم سعی می کنیم در حد توان دانش آموز جنبه های گوناگون عدد 3 را برای او مطرح سازیم . به شکل زیر که قسمتی از یک شبکه مفهومی است توجه کنید:

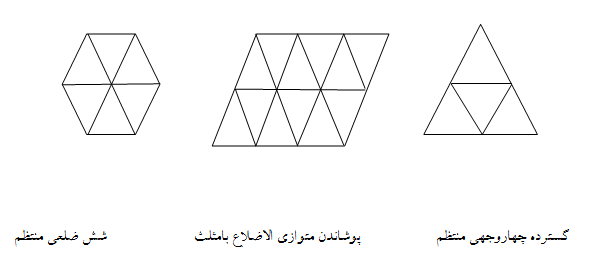
همانطور که در نمونه بالا مشاهده می شود ، مفهوم عدد3 مفهومی هندسی مثل مثلث و مفهوم کسر و کاشی کاری پیوند می خورد. در چنین برنامه ای بحث های گوناگون ریاضی مثل حساب و هندسه از هم تفکیک و جدا نمی شود. به عبارت دیگر همان زمان که عدد3 معرفی می شود،مثلث و کسر⅓ نیزمطرح می گردد و از دانش آموز خواسته می شود با شکل های مثلثی الگوهای متفاوتی بسازند، از جمله اینکه با 6 مثلث می توان یک شش ضلعی منتظم درست کرد و یا با مثلث ها یک شکل هندسی ایجاد کرد.

    آنچه در خصوص مفاهیم و مهارت ها اهمیت دارد، این است که همیشه و در تمام برنامه درسی باید جاری و ساری باشند. به عبارت دیگر وقتی مفهومی شروع می شود نباید در حد چند صفحه مطرح و سپس ناپدید شود. بلکه در دروس و مفاهیم بعدی باید جاری باشد و ارتباطش با بقیه حفظ شود. همچنین مهارت ها باید درس به درس گسترش یابد  و در یک حرکت به هم توسعه پیدا کند و از درس به درس یا پایه تحصیلی به پایه دیگر انقطاع نداشته باشند.

    این موضوع در کتاب های در حال تألیف ریاضی دبستان مورد نظر قرار گرفته است. در حال حاضر نیز معلمان عزیز دوره ابتدایی می توانند با توجه به نکات ذکر شده خلأهای موجود در کتاب درسی را با ارائه نمونه فعالیت ها و تمرین های مناسب پر کنند و بکوشند بین مفاهیم کتب درسی موجود ارتباط برقرار سازند. برای مثال هنگامی که مفهوم تساوی مطرح می شود،این مفهوم را از ابعاد متفاوت عددی یا جبری و هندسی بررسی کنند.

   (برقرار بودن دو طرف از نظر عددی)  تساوی عددی 5=2+3

 

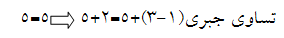
اگر به دو طرف تساوی مقادیر مساوی اضافه کنیم،باز هم تساوی برقرار است.

تساوی هندسی یعنی مساوی بودن دو شکل هندسی(قابل انطباق بودن)

 

 

 منبع:  داوودی،خسرو،1381،هدفهای مهارتی آموزش ریاضیات،رشد آموزش ابتدایی،شماره 6،صفحه30